这两个问题,应该是电商网站或者说 O2O 业务中最常用的功能。在之前,我也想过该题的解决方法。
第一个问题最简单的方法就是,一个 for 遍历周围所有的数据。通过欧式距离的判断,进行从小打大的排序判断,然后推送结果给用户。但是,当商铺基数足够大的时候,似乎,每次的 O(N) 操作,都是一个不小的时间开销。于是,可以通过进行地区的划分进行优化。
比如在二维坐标系中,划分为 N * N 的正方形区域。进行距离判断的时候,只需要查询用户当前区域和周围 8 个区域的店铺,然后进行搜索,然后排序。同时,也可以针对每个区域进行 cache,因为某个区域间的商铺的排序顺序基本不会有太大变化,而且即使是不同的距离,基本也就是 50 ~ 100 米的误差,某种程度上,用户也能接受这样的误差。
所以,这个角度看,似乎是个不错的解决方案,毕竟通过后台的距离判断可以进行离线操作,然后将结果显示到用户端,因为缓存的原因,查找效率也是 O(1)。而且因为是离线的计算,后续的店铺推广业务,广告业务,竞价排名等操作也能很好的集成到离线操作中。
但是,就纯粹的查找效率而言,GEO HASH 似乎是个更好的手段。他的主要思想就是把二维的地理坐标信息投射到一维的坐标轴中。差不多就像这样:
不过具体的实际操作中,也可以是这样的顺序:
这就很好玩了。但是,从业务上来看的话,究竟选取这个还是之前那个,个人还是偏向之前的算法。因为那个是我大学刚毕业那会给出的面试解法。
然后就是更加好玩的找店铺最多的点的算法了。这个问题的由来是这样的,在打Offer 收割赛的时候,遇到了最后一题『剑刃风暴』,这里面的需求就是求如何通过一个固定半径的圆,尽可能多的伤害到尽可能多的英雄。
其实这个业务场景和 O2O 中的,查找最热地区有点类似。通常的解法,就是选点进行判定。比如二维坐标系中的 X, Y, 分别取 delta=0.1 然后进行遍历。最后求出最多的那个点。
To be honest, 这个方法必然是 TLE 的而且也不准确。因为,最后的精度完全取决于你的 delta 取值。
其实有个更好的解法,可以参考 POJ 1981 这道题的解法。
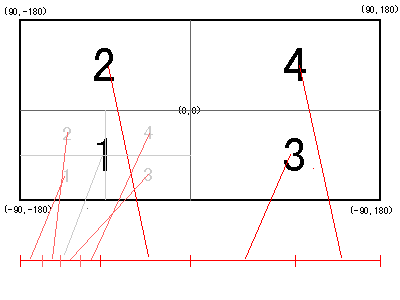
先固定一个点 i,该点的单位圆与其他点 j 的单位圆相交,形成 i 圆上的一段弧,该弧被 j 圆覆盖。最终圆如果在该弧上,则一定能覆盖 j 点。那么问题归结于找出i圆上被覆盖次数最多的一段弧。
至于弧的表示,用两个极角表示,分别为起始和终止,类似于一个区间。枚举完其他点之后,得到 N-1 个区间。将其排序后,从前往后扫描,碰到起始计数 +1,碰到终止计数 -1,同时更新答案。
极角的求解:
以上摘自码农场
所以,最后也能的出一个比较好的结果。不过仔细想来,如果要在业务中,常常进行这样的实时运算。似乎并不是一个最优解。这样的计算非常消耗计算资源。如果貌似不是很好的和 GEOHASH 算法进行集成。如果你的业务中已经集成了 GEOHASH,那么这个思路并不能很好的集成你之前的工作。
所以,如果你一开始就按照划分区域的方法。那么可以同样的进行区域中的店铺数量排序。然后可以快速的进行离线计算。然后当用户进行查询的时候,可以直接 O(1) 返回结果。似乎是个简单而且不是特别低效的方法。这个也是我大学毕业时,给出的解决思路。因为这两个问题是一起提出的。所以不得不给出这样一个在两个问题单独拿出来时并不最优的解,但是,整体看的话,我觉得,还算是个不差的结果。
不过,因为本人的能力有限,并不能很好的结果这两个问题。
如果有更好的解法,望不吝赐教。