算法-卡特兰数(组合数学)

常见的问题，HDOJ 1133

他的递推关系式为:

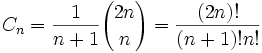
几种常见的题目类型:

• 括号化

  • 矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？

• 出栈顺序

  • 一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?

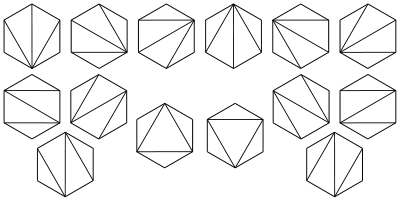
• 突多边形三角划分(握手问题)

  • 在一个凸多边形中，通过若干条互不相交的对角线，把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n，求不同划分的方案数f(n）。
  • 圆桌周围有 2n个人，他们两两握手，但没有交叉的方案数。
  • 

• 给定节点组成二叉树

  • 给定N个节点，能构成多少种不同的二叉树？

• 拥有n+1个叶子节点的二叉树数量

  • 4个叶子节点的所有二叉树形态
  • 

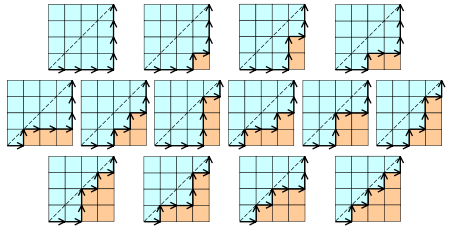
• n*n的方格地图中，从一个角到另外一个角，不跨越对角线的路径数

  • 4×4方格地图中的路径有:
  • 

• 接下来是几道笔试题：

  • 先来一道阿里巴巴的笔试题目：说16个人按顺序去买烧饼，其中8个人每人身上只有一张5块钱，另外8个人每人身上只有一张10块钱。烧饼5块一
    个，开始时烧饼店老板身上没有钱。16个顾客互相不通气，每人只买一个。问这16个人共有多少种排列方法能避免找不开钱的情况出现。
    > C8=1430，所以总数=1430×8!x8！
  • 在图书馆一共6个人在排队，3个还《面试宝典》一书，3个在借《面试宝典》一书，图书馆此时没有了面试宝典了，求他们排队的总数?
    > C5=30,所以总数为: 5×3!x3！=180.